G is de weerstand die C^2 ondervindt .

Waar C^2 bestaat , is er een weerstand G . ( Als C^2 niet bestaat dan is er ook geen weerstand G ) .

Hierdoor kan de C^2 nooit het ultieme bereiken , waar er geen ruimte is , waar de tijd volledig stil staat.

Door het bestaan van C^2 is er de ruimte , afstand , tijd , het heelal .

Als C^2 niet bestaat , dan is er ook geen ruimte , geen tijd , dan is er het tijdloze.

Hierdoor is het dat C^2 gevangen zit in zijn eigen creatie .

C^2 kan niet buiten de ruimte treden , kan niet buiten het heelal treden .

Waar C^2 bestaat , is er ruimte , en tijd , enz.

C^2 is geen wet maar de uitwerking van alle wetten .

En deze zijn onveranderbaar en zonder begin of einde ,

waardoor de uitwerking ( C^2 ) ook eeuwig zal blijven.

Maar C^2 is ook overal in de ruimte aanwezig , want waar C^2 niet is , daar is geen ruimte.

De maat voor de ruimte ( DIM ) is er door de verhouding DIM = C^2 / G .

In het heelal dat een fysiek bestaan heeft , kunnen zich grotere C^2 concentraties voordoen

waardoor de ruimte is samen getrokken en waar de tijd trager verloopt ( op deze plaats ) .

Vandaar de dimensies DIM’s ,

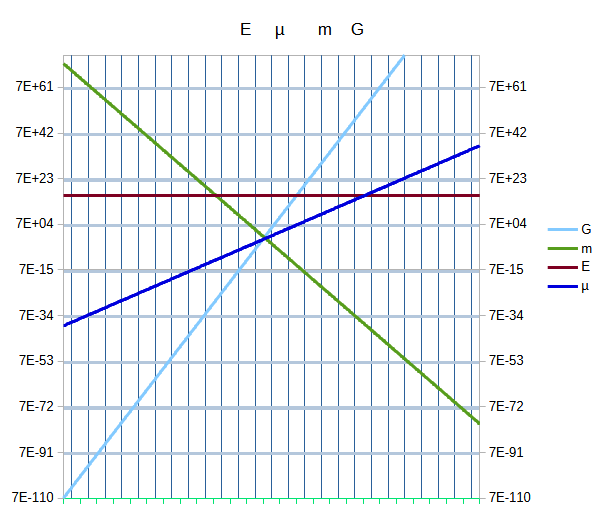
Werking van     E      µ      G    en     materie

Wanneer er in een bepaalde dimensie een hoeveelheid  energie    E     aanwezig is ,

dan is er vorming van materie .Energie is het gereedschap ,  waarmee de wet zich uit.

Waar    E     in het heelal aanwezig is daar is er de materie , meer E  =  meer materie.

In een bepaalde dimensie DIM  waarin een bepaalde  C^2  heerst     is de M materie  =  E  /  C^2

in de formule is zeer duidelijk af te lezen , dat  alleen de energie E  ,  verantwoordelijk is voor

de materie in een bepaalde C^2     DIM.

Wanneer bij dezelfde C^2  (DIM) meer E aanwezig is , dan zal er ook meer materie zijn.

Wat E is voor C^2   ,   is µ voor G.       µ en G zijn de reacties op E en C^2.

E en µ verhouden zich zoals C^2 en G.      E/µ  =  C^2/ G

Hieruit volgt     µ = E * G / C^2       

E = M materie * C^2        >>>>>> M materie = E / C^2      >>>>>     µ = materie * G

M materie     =      µ  *  G    =      E / C^2

Een materie met een bepaalde verhouding  E/µ zal steeds in de juiste DIM aanwezig zijn waar E/µ = C^2/G

Als de verhouding niet hetzelfde is zal deze materie een snelheid ontwikkelen , die afhankelijk is

van het verschil in hun verhoudingen.

Deze snelheid zal  0  zijn als deze materie in de juiste DIM is.

Materies met dezelfde verhoudingen , willen steeds op dezelfde plaats zijn.

Dit veroorzaakt de gravitatie  µ .

Door het bestaan van materie  is er gravitatie   µ    ( aantrekking tussen de materie ) , deze gravitatie  bestaat niet als er 

geen materie is .

De gravitatie µ en de  energie E zijn steeds in dezelfde verhouding aanwezig  als  de  C^2   en de  G.

In een bepaalde  DIM   waarin een bepaalde   G   heerst is de     µ = E * G / C^2

Het is perfect mogelijk om de materie te berekenen met de gravitatie µ     m materie = µ / G

Maar het is de  energie E die verantwoordelijk is voor het bestaan van de materie.

µ de gravitatie ,  is een reactie op de  energie  E   en is dus niet rechtstreeks verantwoordelijk voor de materie.

Zo hebben we dan twee manieren om de materie te berekenen   m = E / C^2               m = µ / G 

Hieruit volgt    E / C^2    =    µ  /  G               of           E  /  µ      =      C^2  /  G     de materie kan alleen bestaan

in een dimensie    ( ruimte )   die  overeenkomstige eigenschappen heeft.

een DIM  waar  C^2 / G   =   E  /  µ   .

Als er kleine  verschillen  zijn    vb  een kleine overschot van  E   

dan zal dat verschil zich uiten in beweging , snelheid .

Hoe groter de materie hoe groter is de µ  (gravitatie)      µ = m materie *  G   ( in dezelfde DIM)

 C^2   en   G       vormen de ruimte

E         en   µ       vormen de materie.

Als C^2 niet bestaat dan is G ook onbestaande ,    als   E   niet bestaat dan is   µ   ook onbestaande.

Dan is er ook geen materie.

E     µ     C^2     G     zijn geen wetten , maar zijn de uitwerkingen van de wetten ( tijdloos ) .

Deze zullen ook eeuwig bestaan vermits de wetten zelf , geen begin of einde hebben , in het tijdloze , en onveranderlijk zijn.

oef , hieruit kan ik besluiten dat het heelal eeuwig is.

C^2    en    G     bepalen het tijdverloop ,    als    C^2    het ultieme zou kunnen bereiken dan zou de tijd stil staan ,

maar dát is niet mogelijk vermits C^2 binnen de ruimte bestaat en er steeds de tegenwerking G  is.

Het zijn de verhoudingen C^2 / G die het tijdverloop bepalen , dus iedere DIM draagt een eigen tijdverloop in zich.

Dat is ook de reden waarom er in iedere DIM verschillende lichtsnelheden gemeten worden.