Er is enkel licht nodig voor ons bestaan.
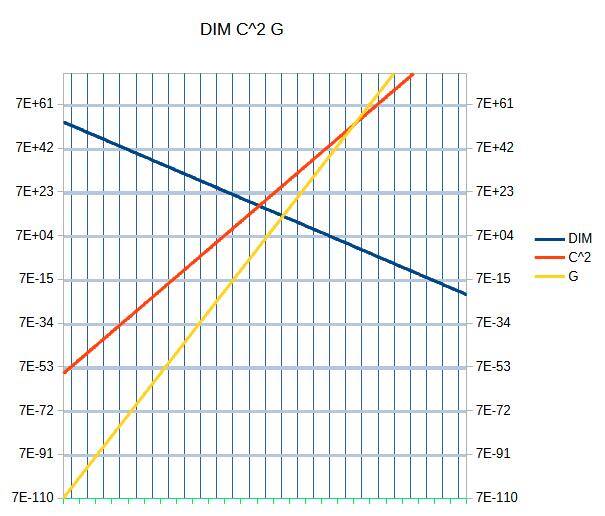
Dimensie’s zijn verhoudingen van C^2 en G G is een tegenreactie op C^2 ,
Geen C^2 Geen G. C^2 en G zijn onafscheidelijk.
Daaruit volgt , geen C^2 >>> geen ruimte , ( geen DIM ) Hoe groter C^2 hoe groter G (en omgekeerd ).
Maar hoe kleiner C^2 en G , hoe groter de DIM’s . Hoe dichter C^2 de zero nadert , hoe groter is de DIM . ( de ruimte )
Dit geeft ons een aanwijzing over, de manier waarop wij ons in het heelal , het tijdloze moeten voorstellen .
Het is niet 100% juist , maar het is een manier , een hulpmiddel , om een beeld te hebben van het tijdloze.
De wetten , die eveneens tijdloos zijn , nemen geen plaats in , zijn niet afhankelijk van plaats of tijd.
Daarom juist kunnen zij in het heelal , op elke plaats en op elk ogenblik , optreden.
Wij nemen de wetten , zelf , niet waar , omdat ze vormloos , tijdloos voor ons onzichtbaar .
Hun uitwerkingen , ongelofelijke sterke krachten die er ontwikkeld worden , zijn constant en overal zichtbaar.
Voor ons , in ons heelal kunnen we een plaats aanwijzen , want elk plaatsje ( voor ons ) dat je aanduid is juist .
Op ieder plaatsje in het heelal zijn alle wetten ( zij "zijn" ) , op elk ogenblik , en voeren hun logica uit.
Het bewijs ligt toch voor de hand .
Alles wat bestaat , is er toch door toedoen van de wetten.
De ontelbare zandkorrels op onze aarde bestaan door de uitwerking van de wetten .
Ieder korreltje is er door dezelfde wetten die zich laten gelden op gelijk welke plaats op de aarde en op ieder ogenblik.
Nogmaals , wij proberen eigenschappen van de wetten die we ontdekken te noteren met formules ,
maar deze notaties hebben geen kracht , brengen de wet niet ten uitvoer .
Iedere wet zal onwrikbaar alles uitvoeren volgens zijn eigen logica en zich aanpassen aan elke omstandigheid
ook volgens zijn eigen logica.
De wetten zijn niet afhankelijk van tijd , zijn eeuwig en onveranderbaar ,
waardoor het heelal eeuwig zal bestaan.
Door het tijdloze besta je , en dan voor eeuwig , ofwel besta je niet , en dan ook voor eeuwig.
Door uitwerking van de wetten van het licht , die tijdloos (eeuwig) en vormloos en geen plaats nodig hebben ,
is er het heelal als fysiek bestaan.
Als C^2 zou kunnen gelijk zijn aan nul , dan zou er ook geen DIM , heelal , tijd , bestaan.
Maar C^2 kan nooit zero worden omdat het onafscheidelijk is van G .
Bij lage concentraties van C^2 is de G nog veel lager en is de ruimte nog groter.
( geen C^2 >> geen G >>> geen DIM ) omdat C^2 zich voordoet , hoe klein het ook mogen wezen ,
bestaat de G en is er ruimte DIM.
C^2 kan geen intrede doen in het tijdloze , door de inwerking van G .
C^2 kan ook nooit het ultieme bereiken , waar de tijd volledig stil staat , om dezelfde reden van G .
Daarom kan C^2 niet buiten de grenzen van het heelal treden , waar C^2 is , daar is ook G ,
en samen vormen zij steeds weer de ruimte , het heelal . DIM = C^2 / G
komt een vervolg.